L’esponente di Hurst

L’esponente di Hurst è una misura statistica utilizzata per studiare le proprietà di ridimensionamento e la memoria a lungo termine dei dati delle serie temporali. È particolarmente utile per dedurre le proprietà di una serie temporale senza assumere stazionarietà. L’esponente di Hurst può indicare se una serie temporale è puramente casuale, di tendenza o di ritorno alla media, rendendola utile per convalidare strategie di momentum o di ritorno alla media nei mercati finanziari. L’esponente viene calcolato regredendo gli intervalli riscalati di una serie temporale sull’intervallo temporale delle osservazioni e viene utilizzato per classificare la serie come con ritorno alla media, di tendenza o con camminata casuale. L’esponente di Hurst varia tra 0 e 1, con valori più alti che indicano un trend più uniforme, meno volatilità e meno asperità. È anche legato alle autocorrelazioni delle serie temporali e alla velocità con cui queste diminuiscono all’aumentare del ritardo tra coppie di valori.

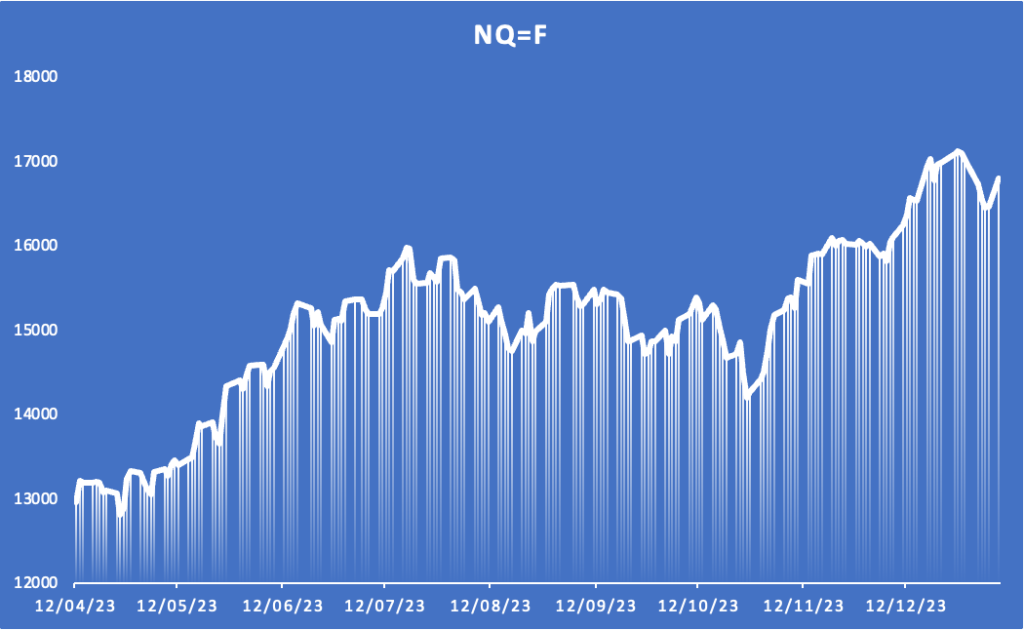
L’esponente di Hurst viene calcolato stimando innanzitutto la dipendenza dell’intervallo riscalato dall’intervallo di tempo dell’osservazione. Ciò comporta la divisione di una serie temporale in una serie di serie temporali più brevi non sovrapposte di diverse lunghezze, quindi il calcolo dell’intervallo medio riscalato per ciascuna lunghezza. Per ciascuna di queste serie temporali più brevi, l’intervallo riscalato viene calcolato trovando la media, la deviazione cumulativa della serie dalla media e la deviazione standard. L’esponente di Hurst viene quindi stimato utilizzando le proprietà di scala della deviazione standard della differenza tra le serie a diversi intervalli temporali, che viene tracciata su una scala log-log per ottenere una linea retta, la cui pendenza fornisce una stima per l’esponente di Hurst. L’esponente di Hurst, indicato come (H), è definito in termini di comportamento asintotico dell’intervallo riscalato in funzione dell’intervallo di tempo. Varia tra 0 e 1, dove un valore di ( H > 0,5 ) indica una serie temporale persistente, ( H < 0,5 ) indica una serie temporale anti-persistente e ( H = 0,5 ) indica una passeggiata casuale o un mercato in cui la previsione degli eventi futuri è difficile quanto prevedere gli eventi passati. Ad esempio, se calcolato sul future del Nasdaq E-Mini, si ottiene un valore di 0.23690719903975105, che indica un comportamento anti-persistente.